(1) 活性炭的基本晶体结构
活性炭由已石墨化的活性炭微晶和未石墨化的非晶炭质构成其基本炭质,非晶炭质与炭微晶的相互连接则构成了活性炭的形状和孔隙结构。活性炭通常被认为是无定形碳,活性炭又被认为是属于微晶类的碳系。 X 射线衍射研究显示,活性炭中包含的石墨微晶是粒径尺寸 1~3 nm 的结晶。根据里利( Riley)的 X 射线分析,除了这些石墨微晶之外, 活性炭通常还包含有有 1~3 个无定形碳以及杂原子, 这些决定着活性炭结构和性质。在石墨结构中,碳原子以大 π 键存在进而形成石墨的平面网状结构,平面网的规律性排列形成规整的三维结构,所以石墨具有导热、导电和润滑等特性。其中, C—C 键长为1.42 Å,面网间距为 3.35 Å,结构如图 1( a)所示。
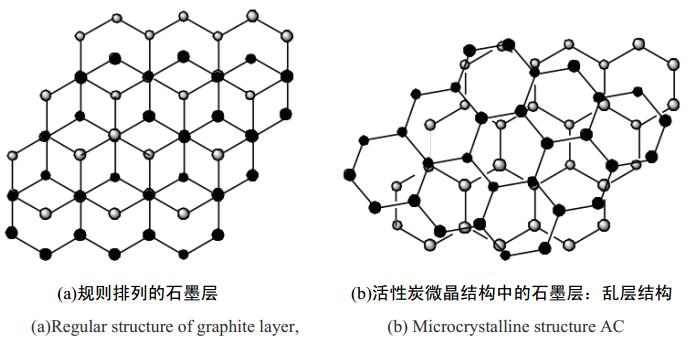
图 1 石墨与活性炭的基本结构与区别
活性炭属于无定形炭的一种,与制备原料(木屑、果壳、煤)相比,由于经过高温炭化、活化等过程,活性炭结构中已形成部分微晶炭,其面网的结构与石墨类似,但是在碳原子六角形排列的完善度、层片大小、平面化程度、 层间距等方面与石墨存在着一定差异。除了微晶炭,活性炭中仍有部分非晶质化的炭, 所以活性炭被认为是由微晶群和单个网状平面以及无规则炭组成的多相物质。通过 X 射线分析,活性炭的炭微晶有两种结构,一种是类石墨结构的微晶炭,其大小受到炭化温度的影响,与石墨相比,微晶炭因平面网之间不整齐排列而出现“乱层结构”。石墨与活性炭的基本结构对比如图 1;另外一种微晶炭是炭六方面网空间交联而形成无序的结构,主要由于石墨网结构之间的轴向不同、 面网间距不整齐、石墨层间扭曲或者杂原子(如氧、氮等)的浸入。 Ri1ey 认为,这两种结构普遍存在于炭材料中,并且直接影响着炭材料的特性。
弗兰克林把除金刚石以外的炭素物质分为容易石墨化的易石墨化炭素和难以石墨化的不易石墨化炭素,如图2 所示,其中, (a)为易石墨化炭素的模型,( b)为难石墨化炭素的模型,不易石墨化的炭素质地较软,易石墨化的炭素质地较硬。他还认为,易石墨化的炭素可能是由乱层结构组成的,而不易石墨化的炭素可能是由具有交叉连锁的晶格结构构成。
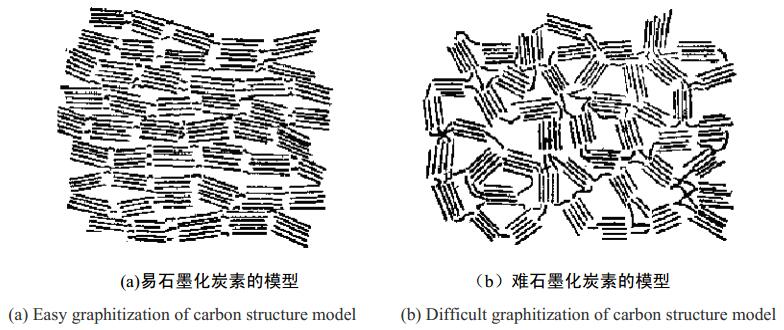
图 2 易石墨化和难石墨化炭素的结构
( 2)活性炭的孔隙结构
① 孔隙结构的形态
无定形炭在活化过程中,其微晶结构间的含碳有机物和无序炭被清除,形成了活性炭的孔隙。活性炭孔隙的形状、大小和分布因原料、炭化和活化过程的不同而有所区别。1960 年,杜比宁把活性炭的孔隙分为大孔(孔径大于 50 nm)、中孔(或称过渡孔,孔 径在 2~50 nm 之间)和微孔(孔径小于 2 nm) 3 类[16],这个方案已被“国际纯化学和应用化学学会( International Union of Pure and Applied Chemistry, IUPAC) ”所接受。这 3类孔隙在活性炭中是相通的,呈现树状的结构,如图3 所示。
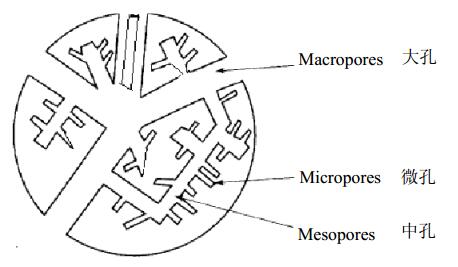
图 3 活性炭的孔隙结构
在杜比宁分类中,大孔能够发生多层吸附,但是由于在活性炭中该类孔隙较少,所以只起到吸附质进入吸附位的通道作用,由于其影响到吸附速度,在应用中也是很重要的因素。中孔或过渡孔不仅起到与大孔相同的作用,同时也起到吸附不能进入微孔的大分子物质的作用。微孔是活性炭吸附作用的主要影响因素,微孔的多少直接关系到吸附能力以及活性炭的比表面积。
② 孔容积计算
孔容积随着活化的进行而增加,孔隙数量决定了孔容积的大小。假设孔隙为圆筒形,在确定比表面积和孔容积的情况下,可利用下式计算孔隙半径:
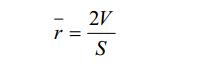
如果孔的形状是由平行平面组成的裂缝状,上式中的孔半径就相当于平面间隔,若假定孔为独立的球状,则上式为:
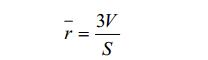
③ 孔径分布的确定
孔径分布是研究活性炭孔径结构的最好手段。通常,采用电子显微镜法、毛细管凝结法、压汞法、分子筛法、 X 射线小角散射法等测定孔径分布。常用的压汞法是利用汞进入孔隙需要一定的压力这一原理,在压力 p 下汞进入半径为 r 的所有孔隙中,通过可以测定由于压力的增加而进入的汞量和各孔径大小,进而确定其孔径分布。如下式:
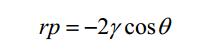
式中, r 为孔半径; p 为汞的压力; θ 为汞的接触角; γ 为汞的表面张力。
( 3)比表面积
吸附是发生在固体表面的现象,所以可以认为,比表面积是影响吸附的重要因素。比表面积的测定方法很多,常用的是 B.E.T 法,此外还有液相吸附法、润湿热法、流通法等等。通过 X 射线小角散射也能测定比表面积,但在活性炭的比表面积中,利用 B.E.T方程来确定多孔材料比表面积是目前最为常用的一种方法。此法测定一般的活性炭的比表面积约为 1000 m2·g-1。 B.E.T 方程表达式为:
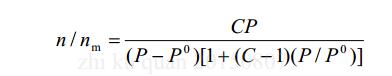
式中, n 为吸附量; nm 为饱和吸附量; Po 为饱和蒸气压; P 为吸附压力; C 为常数。B.E.T 理论需要假定固体表面是均匀的并且同一层分子之间没有相互作用力, 从第二层开始的吸附类似于液化过程。
将上式进行代数变换得:
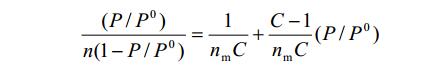
利用线性拟合的斜率和截距,即可求出饱和吸附量 nm。由饱和吸附量可以求出比表面积:
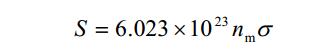
式中: S 为比表面积; σ 为分子的截面积,通常认为 77 K 时氮气分子的截面积为 16.2×10-20m2。
B.E.T 方程的适用范围与吸附质、吸附剂有关,仅适用于吸附等温线的一部分。一般来说,由于吸附剂的适宜相对压力是一定的,如果超出这个范围就会产生一定的偏差。B.E.T 方程是常用的比表面积计算方法,但也存在一定不足:首先,该方法假设了同一吸附层间没有相互作用、上下层分子间存在吸引力。事实上,由于固体表面的不均匀性,个点吸附力也不同,吸附总是优先发生在吸附能有力的位置,所以在孔隙内形成的单分子层不都相同;其次,低压吸附不仅包含有单分子层的覆盖还有微孔的填充,吸附剂表面的不均匀性导致了氮气分子截面积确定的不精确性。尽管 B.E.T 方法存在一定的不足,但是仍被认为是计算比表面积的标准方法。







